Українська вчена В'язовська здійснила прорив у математиці
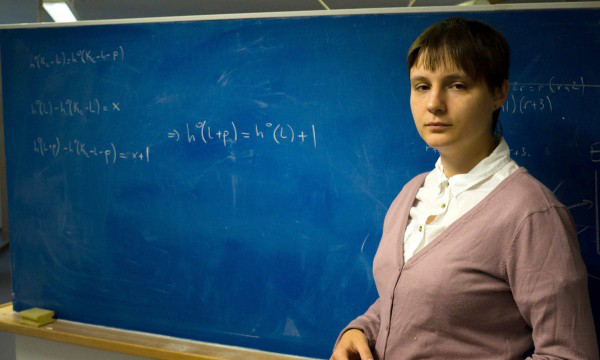
Українська математик Марина В'язовська зі своєю командою знайшла універсальний спосіб, який вирішує цілий клас проблем про те, як найкраще розмістити у 8- та 24-вимірних просторах точки, які відштовхуються одна від одної. Це називають "проривом на рівні видатних математичних відкриттів дев'ятнадцятого століття", – інформує TEXTY.ORG.UA.
Щоб пояснити на фізичних прикладах:
У фізичному світі це може бути, наприклад, "нескінченний" набір електронів, які відштовхуються один від іншого з метою встановити конфігурацію якнайменшої густини.
Або точки, що представляють центри довгих закручених полімерів у розчині, які намагаються не склеїтися докупи.

Таких проблем безліч, і досі було неочевидно, що у всіх їх те саме математичне розв'язання. У більшості вимірів, вважають математики, це не так.
Але виміри 8 та 24 виявилися симетрично конфігурованими. Мовою математики, вони мають "універсально оптимальні" конфігурації.
Раніше В'язовська довела, як найщільніше розмістити сфери однакового розміру у вимірах 8 та 24 – тепер її робота стала більш "загальною".
Наразі виміри 8 та 24 – як і одновимірна лінія – єдині відомі виміри, які мають універсально оптимальні конфігурації. Ще одним кандидатом на таку конфігурацію є рівносторонній трикутник у двовимірній площині, але це не доведено.
Натомість у відомому нам із чуттів тривимірному просторі все не так. Різні конфігурації точок кращі в різних обставинах, а для деяких проблем математики досі не знають, яка конфігурація точок є оптимальною.
"Міняєш вимір або трішки міняєш задачу – й речі можуть стати цілком невідомими. Я не знаю, чому так збудовано математичний усесвіт", – каже Річард Шварц, математик з Браунського університету.
Може здатися дивним, що виміри 8 чи 24 поводяться інакше, ніж, скажімо, виміри 7, чи 18, чи 25. Але математики віддавна знали, що задача оптимального розміщення об'єктів у просторі по-різному працює в різних вимірах.
У тривимірному просторі найкращою є "піраміда апельсинів" (так розміщуються ядра гармат – хоча це робили інтуїтивно задовго до математичного доведення). Подібну "підаміду" можна створити для будь-якого вищого виміру, але зі збільшенням виміру – зростають проміжки між сферами.
Однак у восьмому рівні раптом стає досить місця, щоб нові сфери розміщувати у ці проміжки. Те саме знову відбувається у вимірі 24.
Ці дві математичні гратки (решітки) з невідомих математикам причин є універсальними для різних сфер математики – від теорії чисел до аналізу математичної фізики.
Математики давно на основі непрямих доказів підозрювали, що ці гратки (решітки) є універсально оптимальними, проте не уявляли, як це довести.
У 2016 році В'язовська здійснила перший крок для доведення, а зараз здійснено важливіший, бо більш універсальний доказ.
Команда математиків, які здійснили прорив:

Для довідки:
Українська вчена Марина В’язовська отримала міжнародну "Премію Салема 2016" з математики, яку щороку присуджують молодому вченому за видатні результати досліджень в сфері наукових інтересів Рафаеля Салема, насамперед у теорії рядів Фур'є.
Як зазначається, "Премія Салема" для математиків є аналогом Нобелівської премії.
Комісія присудила премію В’язовській за її відкриття – щодо найщільнішого пакування куль у 8- та 24-вимірних просторах із використанням методів модульних форм.
ЧИТАЙТЕ ТАКОЖ: В Україні стартувала Європейська олімпіада з математики для дівчат
Луцький виш перевіряли через аномальну кількість студентів-призовників
Життя після «МастерШефа»: чим зараз займається волинський кухар Віталій Наливайко та чи знайшов дівчину
Підвищення зарплат педагогам неможливе, – головний освітянин Луцька
У Луцьку хотіли вирощувати банани, але депутати – проти
Нововолинський ремонтно-механічний завод продали: хто новий власник?